Bonjour à tous, voilà mon dernier article publié dans la revue académique Physica Scripta, un nouvel effet découvert qui pourrait permettre d'améliorer les systèmes de guidage ! Comme l'article publié s'adresse à des chercheurs spécialisés dans le domaine et qu'en plus il est écrit en anglais, je vais vous faire un petit résumé :--)
Rotating disk: new physics discovered alongside the Sagnac effect
Mes recherches portent sur la relativité, celle pour la première fois décrite dans les articles d'Albert Einstein en 1905, la relativité appelé restreinte en langue française, pour la différencier de la relativité générale de 1915 qui décrit quant à elle la gravitation. La relativité restreinte introduit la notion d'espace-temps et décrit comment le temps se dilate et les longueurs se contractent entre deux référentiels. L'espace et le temps sont en fait relatifs et l'espace-temps est le nouvel absolu. Ce dernier article utilise la relativité restreinte pour décrire le référentiel tournant. Nous commençons par retrouver un effet déjà connu, l'effet Sagnac, puis nous découvrons un nouvel effet.
C'est quoi l'effet Sagnac ? Vous l'utilisez sans le savoir quand vous prenez l'avion ! La découverte expérimentale a été faite en 1913 par Georges Sagnac. On utilise de nos jours des gyroscopes laser basés sur cet effet qui remplace l'antique boussole et permettent de se repérer bien plus précisément dans l'espace.
Expliquons. Considérez un disque avec une fibre optique sur le périmètre (premier schéma). Si vous émettez un petit flash lumineux en un point de la fibre, la moitié de la lumière va se propager circulairement dans le sens des aiguilles d'une montre et l'autre en sens contraire.
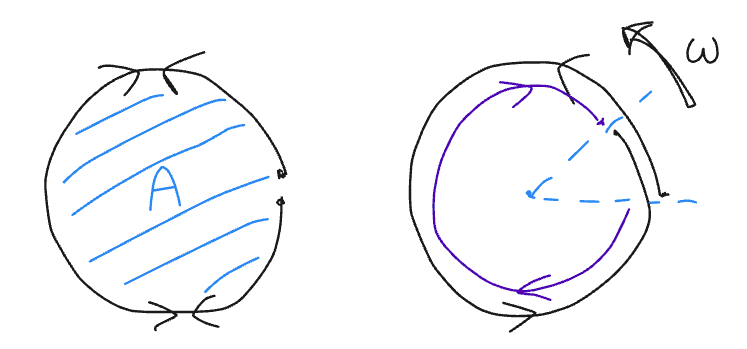
Et, je vous le donne en mille, les deux impulsions lumineuses mettent le même le même temps pour revenir simultanément au point de départ.
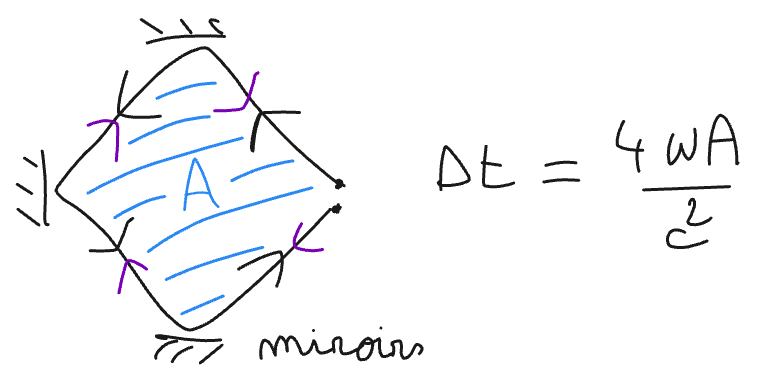
Mais si maintenant le disque est en rotation ? Les impulsions arrivent-elles en même temps ? Laquelle revient en premier au point d'émission ? Vous l'aurez deviné, l'impulsion qui va dans le sens contraire de la rotation du disque ! Le disque vient à elle et cette impulsion a moins de distance à parcourir pour rejoindre le point de départ (deuxième dessin). Le calcul montre que la durée Δt écoulée entre l'arrivée des deux rayons est proportionnelle à l'aire du disque A et à la vitesse de rotation ω. En plaçant ce gyromètre dans un avion, en mesurant Δt on en déduit de quel angle l'avion a tourné.
Étonnamment cette formule reste la même quelque soit la forme du contour et la vitesse v des particules. Par exemple, on sait maintenant fabriquer des lasers avec des atomes qui peuvent avoir des vitesses v très inférieures à la vitesse de la lumière dans le vide c, et on observe le même effet et la même formule qui ne fait pas intervenir la vitesse des atomes v.
Jusqu'à aujourd'hui nous ne connaissions que cet effet Sagnac. Dans cet article il est montré, toujours dans le cadre de la relativité restreinte, qu'il existe un nouvel effet quand la vitesse v devient suffisamment faible.
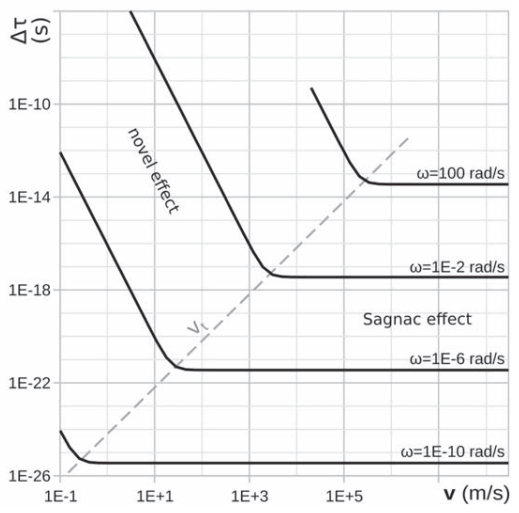
Cette prédiction reste à être vérifiée par l'expérience. Les répercussions pratiques seraient importantes car l'effet est plus fort et permettrait de construire des gyromètres encore plus performants ! C'est important pour les avions, les navires, les sous-marins, les missiles, les fusées, les satellites, etc.
:--D
Pour aller plus loin :
On peut retrouver la formule donnée ici dans le cas du contour circulaire par un calcul qui utilise la mécanique classique. Dans le référentiel R' du laboratoire la lumière va à la vitesse c. Pour le rayon qui tourne dans le même sens que le disque la distance parcourue est ct=2πR+vt, et pour l'autre rayon ct'=2πR-vt' avec v=ωR la vitesse du disque. t et t' sont les temps de parcours de chaque rayons donc Δt=t-t'=2πR/(c-v)-2πR/(c+v)=2πR.2v/(c²-v²). Ce qui donne la formule cherchée avec v très petit devant c.
Dans le référentiel R du disque, on peut récrire les équations de la manière suivante (c-v)t=2πR et (c+v)t'=2πR. Tout ce passe comme si la vitesse de la lumière vallait c dans le référentiel R' du laboratoire et changeait de valeur suivant le sens de parcours dans le référentiel R du disque. Par exemple, dans un train en mouvement rectiligne et uniforme qui roule à la vitesse v, la lumière émise vers vous depuis le quai semblera aller à la vitesse c±v. C'est l'additivité des vitesses. Or on sait que la vitesse de la lumière est la même dans tous les référentiels d'inertie, l'additivité des vitesses n'est pas vérifiée pour la lumière. C'est un fait expérimental qui est pris en compte dans la théorie de la relativité restreinte. Le calcul fait n'est donc pas justifié et il est même étonnant que l'on trouve le bon résultat par ce petit calcul classique. Dans l'article nous retrouvons la formule de l'effet Sagnac en utilisant la relativité restreinte dans le référentiel accéléré du disque tournant. Nous utilisons la métrique adaptée qui permet de faire le calcul exact.
Les calculs réalisés dans l'article considèrent le cas d'un polygone régulier à n cotés et l'on montre que le nouvel effet n'a pas lieu pour un contour circulaire.
L'article de départ, avant relecture par les pairs, qui contient beaucoup plus de détails et d'explications :
Sagnac Effect with Non-Zero Mass Particles and Light: the Transition from Classical to Relativistic



